En el cálculo diferencial, podemos hallar temas sumamente relevantes como es el tema de «Limite», pero ¿No sabes qué es? Cuando se habla del límite de una función hallamos un favor que se manifiesta como F (x), este valor se acerca, a medida que la x se convierte en un número.
¿No comprendes bien de que se trata? Pues bien a continuación te brindamos un ejemplo:
La grafica de X simboliza que estas cerca de un número, de ello puede ser X=8, para ello, debemos comenzar con un punto determinado, donde la x será menor qué el número 8.
Ejemplo de límite de cálculo diferencial
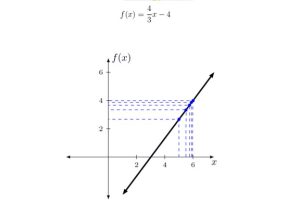
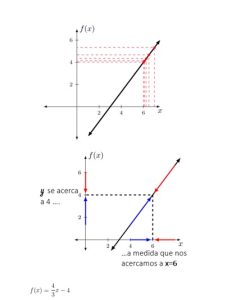
En este ejemplo usamos el número 6 como punto de referencia, si te fijas En el primer recuadro, podemos ver que los valores de X se acercan al No.6, mientras que los valores de Y se van acercando al 4, luego si vemos la segunda imagen, analizamos como x=6 nos crea la función de qué Y=4.
Aunque el tema no sea sorprendente, si genera la idea de que existe un límite.
¿Qué son las Aproximaciones sucesivas?
Las aproximaciones sucesivas en el concepto de límite, pueden comprenderse como cuando alguien te pide que recorrer 10 km, cuando realmente debías recorrer 20 km para llegar al puente, una vez te encuentras en el punto medio, te pedimos que vuelvas a recorrer, y así sucesivamente ¿Consideras que al hacerlo recorrerías la distancia que te separaba de la puerta? Al comienzo sí, pero luego de hacerlo varias veces ¿Qué sucedería?
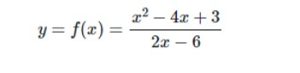
¿Por qué se debe tener cuidado con los límites?
Ahora que ya te explicamos sobre los límites, debes tener en cuenta que hay que observar los limites varias veces, ya que no siempre f (x) = 1 cuando x=0, en este caso, lo que nos dice, es que tenemos la incógnita de F (x), que se acerca a 1, mientras que la x se puede acercar al 0.